Kruskal-Wallis H检验(Kruskal-Wallis H Test)

hyc3140

两组数据的差异比较，我们已经学会采使用t检验和 Mann-Whitney U检验；对于两组以上数据间差异的比较我们采用方差分析（ANOVA）；当多组数据不满足正态性和方差齐性时，我们可以采用Kruskal-Wallis单因素ANOVA分析，对各组资料进行差异比较。

同样，这里给出SPSS操作的具体步骤。首先需要我们录入待分析的数据，数据的录入方式参考之间的教程，都已经很详细的讲过，这里就不赘述，默认已经将待分析的数据录入妥当。

选择【分析】→【非参数检验】→【独立样本】

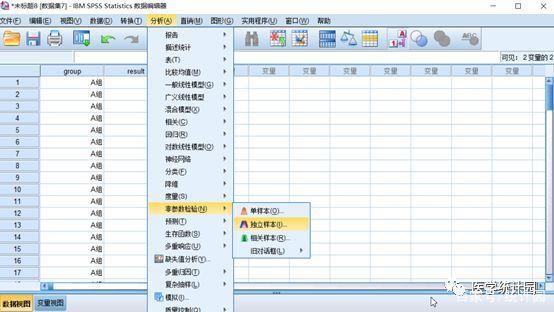
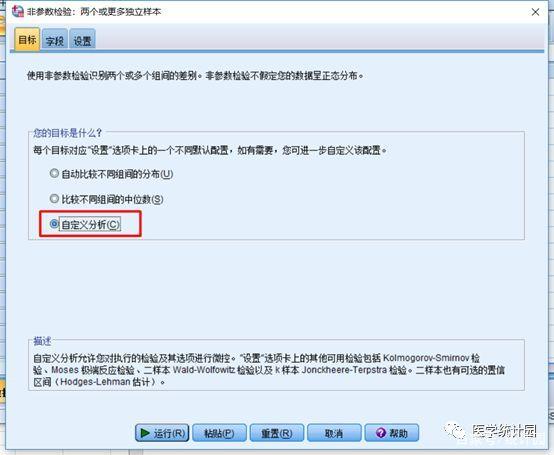
在【目标】界面下，勾选【自定义分析】

在【字段】界面下，将“group”导入【组】，“result”导入【检验字段】

在【设置】界面下，勾选【自定义检验】，在【比较不同组间的分布】中，选择【Kruskal-Wallis单因素ANOVA】，在【多重比较】下拉菜单中选择【所有成对比较】

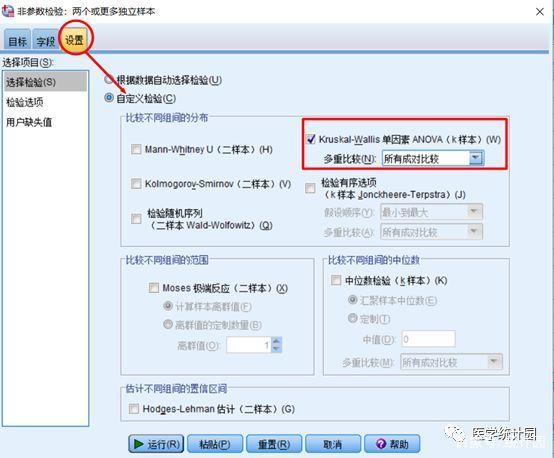
聪明如你，学过之前教程的同学一定会发现，在这个【比较不同组间的分布】菜单界面下，有我们讲过的【Mann-WhitneyU】检验，【Kolmogorov-Smirnov】检验，所以如果你学会了前几节课的教程，这个多组间差异分析对你来讲也是小case

点击【运行】，在弹出【输出文档】查找分析结果

原假设为：result的分布在group类别上相同（H0假设），而Kruskal-Wallis检验的结果表明，显著性水平（即P值）为0.000，故而拒绝原假设，即三组数据差异有统计学意义（P<0.05）。

双击【假设检验汇总】，弹出详细的分析结果

图1 介绍各组的箱型图，表示数据的中位数，上四分位数（75%分位）一级下四分位数（25%分位）；

图2 是对各组数据统计的详细结果，检验统计量为70.40，自由度为2（组数-1），检验结果的P值为0.000。

对于多组间数据的比较，还有一个重要的分析，那就是两两比较！

在【输出文档】最右下角处的【视图】下拉菜单中，选择【独立样本测试图】

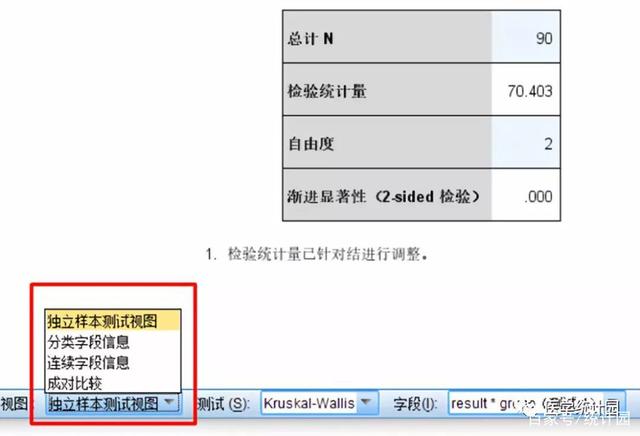
出现3组数据两两比较的结果如下

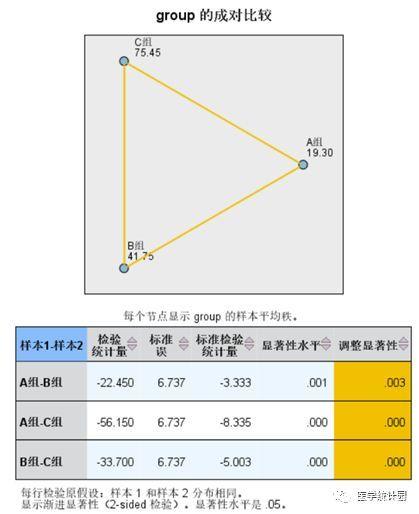
A组与B组相比，检验统计量为-22.45，检验P值为0.003，表明两组数据存在差异，差异有统计学意义（P<0.05）；结合上边的三角图可知，A组的数据是显著低于B组数据；

A组与C组相比，检验统计量为-56.15，检验P值为0.000，表明两组数据存在差异，差异有统计学意义（P<0.05）；结合上边的三角图可知，A组的数据是显著低于C组数据；

B组与C组相比，检验统计量为-33.70，检验P值为0.000，表明两组数据存在差异，差异有统计学意义（P<0.05）；结合上边的三角图可知，B组的数据是显著低于C组数据。